1 2
93 94 95
132 133
Posted: 10/28/2017 5:31 AM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
The prisoner and levers problem lives on, even a week later! Steve Schaefer, a commenter for this page, posted a better strategy in the comment section. I'm not sure if anyone else found this out, because neither us, nor Hector Pefo, nor Riddler, nor Car Talk arrived at this strategy. The strategy gives a way for the 99 non-counting prisoners to flip the tally lever only once, while ensuring the counter does not overcount because of some random starting configuration. It is as follows: Call the levers A and B (A is the tally lever, B the dummy lever). Prisoners 2 through 100 each do the following: - If lever A has not been flipped by the prisoner yet, and the prisoner saw lever A in the up position any time previously, and lever A is down, flip lever A up. Otherwise, flip lever B. Prisoner 1 does the following: - Keep a count starting from 0. If lever A is down, flip lever A up. If lever A is up and Prisoner 1 flipped lever A down on the previous (one before) visit, flip lever A down and add one to the count. Otherwise, flip lever A down and don't add anything. When the count reaches 99, declare that all of the prisoners have been to the room. I ran the expected value calculation and it comes out to be 11096.054 visits, a 45.8% improvement over the other strategy's value of 20476.663. It may even be possible to improve with a different Prisoner 1 strategy of flipping the tally lever (but always flipping the tally lever already seems quite reasonable).
Flip wrote:
... ... ..o .st wx. Which conveniently is 5 remaining, so we can just race 'em. ostwx..........twx Which gives you the 2nd/3rd place in 7 races, deriving the top three: wxy
The result of racing ostwx isn't necessarily twx; it could be wtx, stx, ost, xot, ... (This would of course decide the second and third places.)
Posted: 10/28/2017 7:36 AM
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
Oh god, that 100 prisoner problem is going to haunt me for a while. To take my mind off of it, the horse racing problem is interesting and similar to last week's Riddler Express challenge with the architecture. (Speaking of, I'm annoyed that the official answer indicates you need to confirm the order with Frank at the end, but never mind that.) Ultimately, we have 25 choose 3 = 2,300 possibilities to sift through, since we don't seem to care about the order of the top three finishers. I believe that since each race has 5!=120 ways of being ordered but the finishing position of the last two horses is irrelevant, so each race divides the number of possibilities by no more than 60. Unfortunately, the actual "average reduction in the number of possibilities" must be much lower, since 60 would allow us to answer the question in two races and we know the answer must be at least five since every horse must race at least once. It's a really crappy lower bound. The optimal solution may be some tangled mess of racing horses that have already raced before in an effort to build order as we go along. I guess I can get things started with the first race. There is one way the result could involve all of the top 3 finishers, 20 ways it could include two of the top 3, 20*19/2=190 ways it could include one of the top 3, and 20*19*18/6=1,140 ways it could include none of the top 3. From there, I'm stuck and I don't know how to use this information to investigate further trials. I suspect Flip is on the right track (at least for the official solution, not the optimal one), but that's all I can come up with. The Price is Right question seems like it would be easier to thoroughly investigate, although FractalFusion has warned in the past that game theory problems are too difficult for Riddler challenges. I'll look into it.
Posted: 10/28/2017 8:22 AM
Quote
Flip
Skilled player (1653)
Joined: 7/25/2007
Posts: 299
Location: UK
Sega TAS of 2017 PSX TASer of 2015 PSX TAS of 2015
FractalFusion wrote:
The result of racing ostwx isn't necessarily twx; it could be wtx, stx, ost, xot, ... (This would of course decide the second and third places.)
Yes, those letters were just chosen for convenience. Similarly we could have the outcome of ejoty......tej or w/e. The problem would be symmetrical either way, so the algorithm would still work. For example, as a random selection process, use 2 pangrams. First, the actual speed order which we hope to derive: "Pack my box with five dozen liquor jugs": P<A<C<K<M<Y<B<O<X<W<I<T<H<F<V<E<D<N<L<Q<U<R<J<G<S And then a random race order, say "Sphinx of black quartz, judge my vow" sphin........pmihs.......ihs xofbl.........boxfl........xfl ackqu.......ackqu.......kqu rtjdg.........tdrjg.........rjg emyvw......mywve....wve Race the winners sluge.......elugs......ugs Identifying s as the overall winner, which is correct. Next, use the info from this most recent race to narrow down the potential 2nd/3rd place from the original races. ih. ... ..u .jg ... ihujg.......ihujg.......ujg. Identifying j/g as 3rd/2nd, which is also correct. So this does in fact work in 7 races.
Posted: 10/30/2017 8:34 PM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
Bobo the King wrote:
The Price is Right question seems like it would be easier to thoroughly investigate, although FractalFusion has warned in the past that game theory problems are too difficult for Riddler challenges. I'll look into it.
The game theory problems I was referring to as difficult are mostly games that involve payoff matrices; those games involve players making their choices at the same time. Since the decision to spin the wheel on the Price is Right is sequential (P1 chooses first, then P2 uses prior information to choose, then P3), this problem is easier to understand conceptually than those involving payoff matrices. It's just a matter of working backwards (find P3's strategy, then P2's, then P1's). The optimal strategy for spinning the wheel has already been discussed on many sites so you can just look it up if you want to see what it is.
Posted: 11/3/2017 12:38 PM
Quote
Warp
Banned User
Joined: 3/10/2004
Posts: 7698
Location: Finland
Is it possible to have two functions f(x) and g(x) such that lim(x->a) f(x) = 0, lim(x->a) g(x) = 0 lim(x->a) f(x)g(x) = 0 and f(x) is not just the constant 0 (nor reduces to the constant zero, ie. eg. "f(x)=x-x" would be too boring of an answer)?
Posted: 11/3/2017 5:59 PM
Quote
OmnipotentEntity
He/Him
Player (36)
Joined: 9/11/2004
Posts: 2631
Warp wrote:
Is it possible to have two functions f(x) and g(x) such that lim(x->a) f(x) = 0, lim(x->a) g(x) = 0 lim(x->a) f(x)g(x) = 0 and f(x) is not just the constant 0 (nor reduces to the constant zero, ie. eg. "f(x)=x-x" would be too boring of an answer)?
We can transform lim(x->a) f(x)g(x) into lim(x->a) exp(g(x) / (1 / ln(f(x)))) which is a 0/0 indeterminate form. So we can ask is it possible to find a pair of functions such that lim(x->a) exp(g(x) / (1 / ln(f(x)))) = -infinity ? And the answer is yes. Because we know that lim(x->0) -x / x3 = -infinity. So we just need to set g(x) to -x and we set 1/ln(f(x)) = x3 which gives f(x) = exp(x-3) f(x)^g(x) However, f(x)'s limit at 0 is not two sided. But I bet you can find an example where all limits are two sided armed with this method. (There's a simple example very close in form to the example I gave.)
Build a man a fire, warm him for a day, Set a man on fire, warm him for the rest of his life.
Posted: 11/3/2017 7:33 PM
Quote
Flip
Skilled player (1653)
Joined: 7/25/2007
Posts: 299
Location: UK
Sega TAS of 2017 PSX TASer of 2015 PSX TAS of 2015
Riddler Classic A typical path can be described as 2211221222111 etc. Given n leaps of size 2, this covers total length 2n, thus leaving the remaining 20-2n leaps for size 1, for a total of n+(20-2n)=20-n leaps total. Thus a path with a given amount n of 2-leaps can be ordered in (20-n)Cn ways. Since we can have a maximum total of 10 leaps of size 2, this gives a grant total T=Sum{n=0,10} (20-n)Cn = 20C0+19C1+18C2+....+10C10 =1+19+153+680+1820+3003+3003+1716+495+55+1 =10946 But for jumping with more than two potential leap sizes, dunno.
Posted: 11/3/2017 9:15 PM
Quote
Warp
Banned User
Joined: 3/10/2004
Posts: 7698
Location: Finland
OmnipotentEntity wrote:
And the answer is yes. Because we know that lim(x->0) -x / x3 = -infinity. So we just need to set g(x) to -x and we set 1/ln(f(x)) = x3 which gives f(x) = exp(x-3)
That seems to indeed work.
Posted: 11/3/2017 10:54 PM
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
Flip wrote:
Riddler Classic A typical path can be described as 2211221222111 etc. Given n leaps of size 2, this covers total length 2n, thus leaving the remaining 20-2n leaps for size 1, for a total of n+(20-2n)=20-n leaps total. Thus a path with a given amount n of 2-leaps can be ordered in (20-n)Cn ways. Since we can have a maximum total of 10 leaps of size 2, this gives a grant total T=Sum{n=0,10} (20-n)Cn = 20C0+19C1+18C2+....+10C10 =1+19+153+680+1820+3003+3003+1716+495+55+1 =10946 But for jumping with more than two potential leap sizes, dunno.
I obtained the same value in a slightly different way and I believe I can do other leap strengths as well. There's one way to reach a lily pad one unit away (jump one lily pad forward). There are two ways to reach a lily pad two units away (jump two lily pads forward or jump one lily pad forward twice). For three lily pads, you can enumerate all three directly or you can notice that the frog will first have to reach either the first or second lily pad. It could either jump two units from the first lily pad or jump one unit from the second lily pad. In other words, if we label the number of ways to reach the kth lily pad nk, we have n3 = n1 + n2 = 1 + 2 = 3. You can probably see where I'm going with this. The frog could reach the 4th lily pad from the 2nd or 3rd lily pad and could reach the 5th lily pad from the 3rd or 4th. It should be quickly apparent that nk = nk-2 + nk-1 where we initially have n1 = 1 and n2 = 2. This defines the Fibonacci sequence (offset by one). Simply add them up to find n20 or use your favorite formula or other tools. In my case, I just looked it up on OEIS. The 21st Fibonacci number corresponds to the 20th lily pad and this value is 10946, in agreement with your answer. We can quickly generalize this to hops of any length by defining a new recurrence relation. I'll leave that to you, if you're interested. Riddles were super easy this week.
Posted: 11/4/2017 12:02 AM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
Warp wrote:
OmnipotentEntity wrote:
And the answer is yes. Because we know that lim(x->0) -x / x3 = -infinity. So we just need to set g(x) to -x and we set 1/ln(f(x)) = x3 which gives f(x) = exp(x-3)
That seems to indeed work.
The function f(x) given above does not have a (two-sided) limit as x->0. The one I came up with was f(x)=exp(-x-4), g(x)=x2, and a=0. In this case, f(x), g(x) and f(x)g(x) all have the (two-sided) limit 0 as x->0.
Bobo the King wrote:
Riddles were super easy this week.
Sure was. This was the easiest since a very long time ago, if ever. Both Riddler problems are pretty much known to every math enthusiast (the first is Nim, the second is one of the characterizations of the Fibonacci sequence). As if that wasn't enough, Riddler Express ended up linking to the Nim Wikipedia page which tells you exactly how to solve it. The Riddler Classic generalization is a little more interesting (the frog can jump up to n steps, instead of just 2), but anyone can just write a computer program (or even just use an Excel spreadsheet) to figure it out. The most interesting thing I found out was concerning the growth rate of each sequence depending on n. For n=2, the growth rate is exponential with a base of (1+sqrt(5))/2 (the golden ratio); this is a known property of the Fibonacci sequence. As n grows larger, the base grows; however, the limit of the bases is 2 as n goes to infinity (if you sum all past terms, you get the powers of 2). The base is just the largest real root of xn-xn-1-xn-2-...-x-1, or in other words the largest real solution to (x-2)xn=-1. From this equation, it is clear that x must be less than 2. Approximate bases are as follows: n=2: 1.61803 n=3: 1.83929 n=4: 1.92756 n=5: 1.96595 n=6: 1.98358 n=7: 1.99196 n=8: 1.99603 n=9: 1.99803 n=10: 1.99902 Edit: Changed "exponent" to "base". I still say stupid stuff sometimes. Edit 2: Fixed f(x).
Posted: 11/5/2017 9:46 PM
Quote
OmnipotentEntity
He/Him
Player (36)
Joined: 9/11/2004
Posts: 2631
FractalFusion wrote:
Warp wrote:
OmnipotentEntity wrote:
And the answer is yes. Because we know that lim(x->0) -x / x3 = -infinity. So we just need to set g(x) to -x and we set 1/ln(f(x)) = x3 which gives f(x) = exp(x-3)
That seems to indeed work.
The function f(x) given above does not have a (two-sided) limit as x->0. The one I came up with was f(x)=exp(-x-4), g(x)=x2, and a=0. In this case, f(x), g(x) and f(x)g(x) all have the (two-sided) limit 0 as x->0.
I had mentioned this, but because it was below the picture I guess it was overlooked. I had already known it wasn't a two-sided limit. But I had lobbed the question back to Warp to try to find the solution you found.
OmnipotentEntity wrote:
However, f(x)'s limit at 0 is not two sided. But I bet you can find an example where all limits are two sided armed with this method. (There's a simple example very close in form to the example I gave.)
Build a man a fire, warm him for a day, Set a man on fire, warm him for the rest of his life.
Posted: 11/5/2017 10:27 PM
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
To keep my brain sharp, I've revisited an old Riddler challenge. In particular, I was interested in modeling the Riddler Classic challenge here as a Markov chain. I was successful, after a number of hours of work. I'm having trouble understanding the posted solution, though. What do the variables there represent? Since they work toward ABCD = 9, it would seem that they represent an average number of turns to reach state AAAA, but I'm having trouble seeing exactly how the equations reflect that fact. Is there a general name for this procedure? I began by drawing up the directed, weighted graph corresponding to the Markov process, similar to how it was outlined in the posted solution. I also included a "sink" corresponding to a "game over" state so that values wouldn't accumulate in the state AAAA. This meant that I could calculate the probability directly from powers of the matrix without needing to subtract the previous power. Here's the matrix I came up with: You can verify that these correspond to the probabilities of going from/to the states ABCD, AABC, AABB, AAAB, AAAA, and the "null/game over" state respectively. There's a problem. This matrix is not diagonalizable because the eigenvalue 0 has an algebraic multiplicity of 3 but a geometric multiplicity of 2. After staring at this for a long while, I determined that for the specific initial state of ABCD, the probability of finding the balls in state AAAB is always exactly twice the probability of finding them in state AABB. This allows you to combine those variables into one. I also discarded the ABCD row and column to the matrix since it will immediately leave that state. (As we'll see in a minute, that means we have to be a little careful with our powers.) Here's the new matrix: That's much easier to work with and it is diagonalizable. The average number of turns until the game ends is then: Where we multiply from the left by [0, 0, 1, 0] because we're interested in the state AAAA and we multiply from the right by [1, 0, 0, 0] because that is the initial state. Writing a few terms of the sum out explicitly, it becomes apparent that this is a variant of the geometric series. We merely need to take our diagonal matrix of eigenvalues and replace them with x*(2-x)/(1-x)^2, where x represents each eigenvalue. One of our eigenvalues is 1, giving an infinite entry in our diagonal matrix. This entry is later multiplied by zero which apparently nullifies it (since I obtained the correct answer). I'll leave the details of the proof to whoever's following along. I also tried repeating the proof with a new matrix that doesn't have a "sink" defined in it: Writing out the average number of turns in terms of this matrix results in something based directly off of the geometric series. The problem then boils down to computing C*(C-1)-1, where 1 is the identity matrix. Unfortunately, C-1 is not invertible, so I stopped my attempt at a proof there. On the other hand, my original proof had an infinity in it and I was able to get around that, so I wonder if the same is possible here. Anyway, what I'm really curious about is what the Riddler's official solution is trying to say and whether this procedure is general.
Posted: 11/6/2017 2:38 AM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
Bobo the King wrote:
What do the variables there represent?
The variables are expected values. More specifically, EABCD, EAABC, EAABB, and EAAAB are the expected number of turns required to go from state ABCD, AABC, AABB, AAAB (respectively) to state AAAA. The following relations apply to these values: EABCD=1+EAABC, EAABC=1+(6/12)EAABC+(4/12)EAAAB+(2/12)EAABB, EAABB=1+(4/12)EAABB+(8/12)EAAAB, EAAAB=1+(6/12)EAAAB+(3/12)EAABB+(3/12)(0). Then one can solve this to get EAAAB=5.5, EAABB=7, EAABC=8, EABCD=9. The expected number of turns to go from ABCD to AAAA is 9. That's what the Riddler is trying to say.
Posted: 11/8/2017 4:26 AM
Quote
OmnipotentEntity
He/Him
Player (36)
Joined: 9/11/2004
Posts: 2631
Using latex notation. Sorry about how messy it is. This post rendered as a document: Page 1 Page 2 Let's say that we have an integral: $$\int \cos(\omega x) \mathrm{e}^{a x} dx $$ One method of working this integral is to use integration by parts twice to obtain a copy of the original integral, but that's long and kind of annoying: $$\begin{split} \int \cos(\omega x) \mathrm{e}^{a x} dx &= \frac1{a} \cos(\omega x) \mathrm{e}^{a x} - \int -\frac{\omega}{a} \sin(\omega x) \mathrm{e}^{a x} dx \\ &= \frac1{a} \cos(\omega x) \mathrm{e}^{a x} + \frac{\omega}{a} \int \sin(\omega x) \mathrm{e}^{a x} dx \\ &= \frac1{a} \cos(\omega x) \mathrm{e}^{a x} + \frac{\omega}{a} \left(\frac1{a} \sin(\omega x) \mathrm{e}^{a x} - \int \frac{\omega}{a} \cos(\omega x) \mathrm{e}^{a x} dx\right) \\ &= \frac1{a} \cos(\omega x) \mathrm{e}^{a x} + \frac{\omega}{a^2} \sin(\omega x) \mathrm{e}^{a x} - \frac{\omega^2}{a^2} \int\ \cos(\omega x) \mathrm{e}^{a x} dx \\ \left(a^2 + \omega^2\right)\int \cos(\omega x) \mathrm{e}^{a x} dx &= a \cos(\omega x) \mathrm{e}^{a x} + \omega \sin(\omega x) \mathrm{e}^{a x} \\ \int \cos(\omega x) \mathrm{e}^{a x} dx &= \frac{a}{a^2 + \omega^2} \cos(\omega x) \mathrm{e}^{a x} + \frac{\omega}{a^2 + \omega^2} \sin(\omega x) \mathrm{e}^{a x} \\ \end{split}$$ Instead, we can use the complex domain and compute (assuming $$x$$ is real): $$\int \Re\left\{\mathrm{e}^{i \omega x}\right\} \mathrm{e}^{a x} dx $$ And assuming that $$a$$ is also a real number we can bring it into the Real part and compute the integral simply: $$\begin{split} &= \int \Re\left\{\mathrm{e}^{(a + i \omega) x}\right\} dx \\ &= \Re\left\{\frac1{a + i \omega}\mathrm{e}^{(a + i \omega) x}\right\} \\ &= \Re\left\{\frac{a - i \omega}{a^2 + \omega^2} \mathrm{e}^{ i \omega x} \mathrm{e}^{a x}\right\} \\ &= \frac{a}{a^2 + \omega^2} \cos(\omega x) \mathrm{e}^{ax} + \frac{\omega}{a^2 + \omega^2} \sin(\omega x) \mathrm{e}^{a x} \\ \end{split}$$ But if $$a$$ is not a real number then bringing $$\mathrm{e}^{a t}$$ into the $$\Re$$ isn't allowed. But we get the same answer. So if we try to compute the integral in this way it's an abuse of notation. It does work in this instance, and other simple cases like $$x \cos(\omega x) \mathrm{e}^{a x}$$. Because this sort of integrand appears in the Laplace Transform reasonably commonly, it might be useful to know when this sort of abuse will work, and when it breaks down. (Yes, it is possible to also just use the identity $$\cos(\omega x) = \frac1{2} \left( \mathrm{e}^{i \omega x} + \mathrm{e}^{-i \omega x} \right)$$ and while that's easier than the integration by parts, it's more involved than the abuse.) I asked around and most answers I got had to do with complex analysis and the idea of analytic continuation. If we have: $$f(x) cos(\omega x) \mathrm{e}^{a x}$$ Then if $$f(x)$$ is an real-analytic function on the domain of integration then this should be a valid abuse of notation. Is this correct? Or does it need to be complex analytic? Or am I completely off track?
Build a man a fire, warm him for a day, Set a man on fire, warm him for the rest of his life.
Posted: 11/8/2017 7:53 PM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
OmnipotentEntity wrote:
But if $$a$$ is not a real number then bringing $$\mathrm{e}^{a t}$$ into the $$\Re$$ isn't allowed. But we get the same answer. So if we try to compute the integral in this way it's an abuse of notation.
Instead of using Re(eiωx) for cos(ωx), use (1/2)(eiωx+e-iωx) instead. (This follows from Euler's formula.) Then it will work out to be the same answer. This way, we do not need to worry about abuse of notation; it works when a is complex. In fact, it now works even if ω is complex. (Euler's formula holds for complex values as well.) By the way, the image you uploaded isn't visible in imgur without going into expand mode. It may be because the background color is regarded as transparent, even though it should be white. Edit: The image is directly linked now, which solves the problem.
Posted: 11/8/2017 8:32 PM
Quote
OmnipotentEntity
He/Him
Player (36)
Joined: 9/11/2004
Posts: 2631
FractalFusion wrote:
OmnipotentEntity wrote:
But if $$a$$ is not a real number then bringing $$\mathrm{e}^{a t}$$ into the $$\Re$$ isn't allowed. But we get the same answer. So if we try to compute the integral in this way it's an abuse of notation.
Instead of using Re(eiωx) for cos(ωx), use (1/2)(eiωx+e-iωx) instead. (This follows from Euler's formula.) Then it will work out to be the same answer. This way, we do not need to worry about abuse of notation; it works when a is complex. In fact, it now works even if ω is complex. (Euler's formula holds for complex values as well.) By the way, the image you uploaded isn't visible in imgur without going into expand mode. It may be because the background color is regarded as transparent, even though it should be white. Edit: The image is directly linked now, which solves the problem.
I did mention that it works with the cosine formula. I was hoping to use the abuse of notation, provided I knew exactly where it works and where it breaks down.
OmnipotentEntity wrote:
(Yes, it is possible to also just use the identity $$\cos(\omega x) = \frac1{2} \left( \mathrm{e}^{i \omega x} + \mathrm{e}^{-i \omega x} \right)$$ and while that's easier than the integration by parts, it's more involved than the abuse.)
Sorry about the transparency issue, the images were always direct links, but I guess imgur wasn't behaving as I expected.
Build a man a fire, warm him for a day, Set a man on fire, warm him for the rest of his life.
Posted: 11/9/2017 7:44 AM
Quote
Warp
Banned User
Joined: 3/10/2004
Posts: 7698
Location: Finland
I wish somebody would integrate the math plugin into the forum... http://tasvideos.org/forum/viewtopic.php?t=19519
Posted: 11/9/2017 1:57 PM
Quote
OmnipotentEntity
He/Him
Player (36)
Joined: 9/11/2004
Posts: 2631
Warp wrote:
I wish somebody would integrate the math plugin into the forum... http://tasvideos.org/forum/viewtopic.php?t=19519
I'm pretty sure it won't be that easy. I remember back in the day Bisqwit telling me that he couldn't even update to phpbb 3.0 because there was so much backend integration between the site and the forum. All work that would have to be redone. (In fact, I believe we're actually still on phpBB 2.0). The mod I linked is for phpbb 3.0.x so it would need to be reworked for 2.0. It's not as simple as just installing it.
Build a man a fire, warm him for a day, Set a man on fire, warm him for the rest of his life.
Posted: 11/9/2017 8:30 PM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
Seeing how this site is run, I don't think interface changes of any kind will be made any time soon, if ever. To generate online LaTeX images to embed in your posts, use one of the following: https://latex.codecogs.com/eqneditor/editor.php http://latex2png.com/
Posted: 11/10/2017 8:55 PM
Quote
Flip
Skilled player (1653)
Joined: 7/25/2007
Posts: 299
Location: UK
Sega TAS of 2017 PSX TASer of 2015 PSX TAS of 2015
Riddler Express Since we're dealing with hexagons here, sections form nice equilateral triangles. The shaded area in question is one third of its triangle, where the triangle occupies one sixth of the main hexagon, thus the shaded part has area 1/3 x 1/6 = 1/18. Riddler Classic This seems relatively easy, just split it up into a bunch of semicircles. Thus A=A1+A2=(a1-a2+a3)+(a4-a5+a6) =π/2 ( (10+2)2 - (10-2)2 + 22 ) + π/2 ( (5+2)2 - (5-2)2 + 22 ) =π/2 ( 122 - 82 + 22 + 72 - 32 + 22) = π/2 (144-64+4+49-9+4) = π/2 (128) = 64π
Posted: 11/10/2017 11:21 PM
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
Flip wrote:
Riddler Express Since we're dealing with hexagons here, sections form nice equilateral triangles. The shaded area in question is one third of its triangle, where the triangle occupies one sixth of the main hexagon, thus the shaded part has area 1/3 x 1/6 = 1/18. Riddler Classic This seems relatively easy, just split it up into a bunch of semicircles. Thus A=A1+A2=(a1-a2+a3)+(a4-a5+a6) =π/2 ( (10+2)2 - (10-2)2 + 22 ) + π/2 ( (5+2)2 - (5-2)2 + 22 ) =π/2 ( 122 - 82 + 22 + 72 - 32 + 22) = π/2 (144-64+4+49-9+4) = π/2 (128) = 64π
Yep.
Posted: 11/12/2017 1:02 PM
Quote
Warp
Banned User
Joined: 3/10/2004
Posts: 7698
Location: Finland
In his newest video, blackpenredpen tackles the problem: lim(n→∞) (n!/nn)1/n I found it very interesting. Before watching the video, perhaps you could be interested in trying it yourself. (Btw, he didn't need the gamma function to solve it, although I suppose there's no rule that would forbid using it.)
Posted: 11/18/2017 12:48 AM
(Edited: 11/18/2017 5:12 AM)
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
New riddles. Riddle 1: I haven't solved this one, but it's easy to show that with n knights, you need at least (n-1)/2 arrangements to ensure everyone gets a handshake. The total number of handshakes needed is 1/2*n*(n-1) and the maximum number of unique handshakes per arrangement is n (everyone shakes the hand of the person to their left and to their right, which double-counts the number of handshakes). I'll try to see if there's a strategy to obtain this minimum number of arrangements. Riddle 2: This needs some careful interpretation. K is inserted somewhere within the integers 0 through 9, shifting some of the integers up. For example, if K = 3, then 0 remains 0, 1 remains 1, 2 remains 2, K takes the place of 3, 3 becomes 4, 4 becomes 5, and so on, up to 9 becoming 10. I solved this by converting one of the equations from a guess for base keleven to base 11, carefully solving them, and then converting the solution back to my guess for base keleven. One of my guesses worked. Riddle 3: This is the riddle I'm most interested in and I can't make any headway on it. Someone in the comments pointed out, "For Riddle 3, how does any strategy give a nonzero expected score? Am I missing something?" I'm in complete agreement. If my current score is S and the value of the current question is N, then by guessing, I can change my score to either S+N or S-N. If I skip the question, my score remains at S. On the other hand, this reminds me a little of the St. Petersburg lottery or maybe a Martingale betting strategy, both of which give unexpected results. Could someone weigh in with either a different interpretation of the problem statement or a correction to my logic? In the meantime, I'll play around with tests that have just 2 or 3 questions, seeing if I can bring the expected value of your score up from 0. I think there would be some interesting math involved if, say, your score could not be less than 0 or you are attempting to outperform some percentage of other students taking the exam. Riddle 4: This riddle was straightforward with matrices. My first effort was to guess and check, but I cheated just a little with my calculator to find that the answers aren't integers. Then I cheated entirely to see that the answers are horrendous. I highly recommend setting up the matrix and just solving it computationally. The determinant is a two-digit prime number, the numerators of the variables are two- and three-digit numbers, and the numerators of the values under the question marks are four digit numbers... ... with just one exception. The question mark corresponding to the fifth row is 31. I'm trying to figure out exactly why; it should be some simple linear combination of the other five equations. I gave it one good effort but I think my analysis is off. I'll attempt it again. It turns out there's one free variable, so you need to use an augmented matrix and put it in reduced row-echelon form. Edit: I found my error in riddle 4. My reduced row-echelon form was correct, I just made a small math error when plugging in values. We have a free parameter because the value of candy corn is zero. 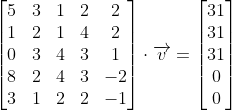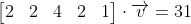Our equations in matrix form are: (The order of the variables here is acorns, candy corn, apples, leaves, pumpkins.) The equation corresponding to the fifth row is: This equation is necessarily a linear combination of the other five equations, which are linearly independent. 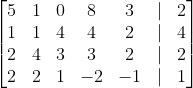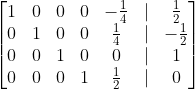Our augmented matrix is then: In reduced row-echelon form, this becomes: Taking the variables to be A, B, C, D, and E, where E is our free parameter, this tells us: So notice that A = -B and C=1. Since the right hand side of the equations corresponding to A, B, and C are all 31 and the right hand side of the remaining equations is zero, this proves that the right hand side of equation from the fifth row is 31. And of course this remains true when we demand that the coefficient of candy corn match up.
Posted: 11/18/2017 3:26 AM
Quote
FractalFusion
Editor, Expert player (2080)
Joined: 6/15/2005
Posts: 3284
Glitchy TAS of 2013 Gameboy TAS of 2013 PSX TASer of 2010
Bobo the King wrote:
Riddle 1: ... the maximum number of unique handshakes per arrangement is n (everyone shakes the hand of the person to their left and to their right, which double-counts the number of handshakes)
The maximum number of unique handshakes per arrangement is far greater than n; a person is permitted to reach across the table to shake the hand of someone not sitting adjacent, provided that arms never cross. The number of possible handshakes per arrangement is not important to this problem though. The problem asks for the number of unique seating arrangements required to get everyone to shake hands, and the answer is ceil(log2(n)), ceil(x) being the least integer that is greater than or equal to x.
Bobo the King wrote:
Riddle 4: ... It turns out there's one free variable, so you need to use an augmented matrix and put it in reduced row-echelon form.
There are 5 equations and 5 unknowns in this problem, and according to my calculation, there is a unique solution. I don't know where this "free variable" is coming in. Did you mean redundant equation? (But there are only 5 equations.) You may possibly be correct that the last row is an integer multiple of some other rows/columns (but I haven't worked out the problem to completion yet so I wouldn't know).
Posted: 11/18/2017 3:44 AM
Quote
Bobo_the_King
Player (80)
Joined: 8/5/2007
Posts: 865
FractalFusion wrote:
Bobo the King wrote:
Riddle 1: ... the maximum number of unique handshakes per arrangement is n (everyone shakes the hand of the person to their left and to their right, which double-counts the number of handshakes)
The maximum number of unique handshakes per arrangement is far greater than n; a person is permitted to reach across the table to shake the hand of someone not sitting adjacent, provided that arms never cross.
Ah! I didn't realize that members could stretch their arms across the table like Dhalsim from Street Fighter. But... then wouldn't the number of arrangements needed be just one? Everyone just sits where they are and then continues reaching across the table through as many rounds as necessary? I've peeked at your answer and I can't quite figure out how you're interpreting this problem.
FractalFusion wrote:
Bobo the King wrote:
Riddle 4: ... It turns out there's one free variable, so you need to use an augmented matrix and put it in reduced row-echelon form.
There are 5 equations and 5 unknowns in this problem, and according to my calculation, there is a unique solution. I don't know where this "free variable" is coming in. Did you mean redundant equation? (But there are only 5 equations.) You may possibly be correct that the last row is an integer multiple of some other rows/columns (but I haven't worked out the problem to completion yet so I wouldn't know).
See the edit to my previous post. The "free variable" comes from the fact that the value of candy corn is zero. This means we don't need to demand that its coefficient match up in our linear combination of the other equations. Edit: Also, any insight into problem 3? Edit 2: I think I see now where the handshake problem becomes nontrivial. It's in the second rule: "During each round of handshakes, every member of LINK must be shaking one and only one hand." This means that you can't decide not to shake a hand and this explains why the two sample number of members were both even values. It also means that two people sitting two seats apart (with one person between them) can't possibly shake hands because the person they span will be cut off from all other handshakes. Incidentally, this means you aren't the only new inductee to LINK. New members are necessarily knighted in pairs (or other multiples of two). All right, I think I can stumble through it from here.
1 2
93 94 95
132 133