
By previous question, at the origin we have a smaller circle of radius r, touching the surrounding five of radius R=1. This gives the interior circle a radius of
r = R*(1/(sin(pi/n))-1=1/sin(pi/5)-1= ~0.7 (Yellow)
Distance from origin to inner circle origin D(O,O
i)=r+R=r+1 (Red)
Distance from inner to outer circle origin D(O
i,O
o)=2R=2 (Green)
Distance from outer origin to outer edge D(O
o,E)=R=1 (Green)
But these are obviously not in the same direction, so to find the overall distance we need a bit of trig. First consider the closest triangle, formed by 2 reds and a green. This is isosceles, and we know the inner angle, thus:
A(O
i,O,O
i)=2pi/5
A(O
i,O
i,O)=(pi-2pi/5)/2=(5pi/5-2pi/5)/2=3pi/10
We know the four inner/outer circles create a square, giving
A(O
i,O
i,O
o)=pi/2
A(O,O
i,O
o)=A(O
i,O
i,O)+A(O
i,O
i,O
o)=pi/2+3pi/10=5pi/10+3pi/10=8pi/10=4pi/5
Now we know this angle, we can use it for the larger triangle O
oO
iO (Green Red Blue). From a
2=b
2+c
2-2bcCos(A), we have
D(O, O
o)
2=2
2+(1+r)^2-2(2)(1+r)Cos(4Pi/5)= ~12.4
D(O, O
o)=L= ~3.52 (Blue)
Next, we have consider triangle O
oOO
o (blue blue green), being isosceles with lengths L, L, and 2R=2. We need the interior angle, so therefore we have
A(O
o,O,O
o)=ArcCos ((b
2+c
2-a
2)/(2bc))=ArcCos ((L
2+L
2-2
2)/(2(L)(L)))=ArcCos ((2L
2-4)/(2L
2)=ArcCos (1-2/L
2)
=~ArcCos(0.84) =~ 0.58 radians.
This gives the other triangles' angles as:
A(O,O
O,O
O)=(Pi-0.58)/2=~1.28 radians.
A(O,O
O,E)=1.28+Pi/2=~2.86 radians.
Finally, consider the triangle going from OO
oE (Blue Green Purple). We know 2 lengths, and one angle (2.86), giving our overall radius D (Purple) to be
a
2=b
2+c
2-2bcCos(A)
D
2=3.52
2+1
2-2(3.52)(1)Cos(2.86)=~20.1
D=~4.49










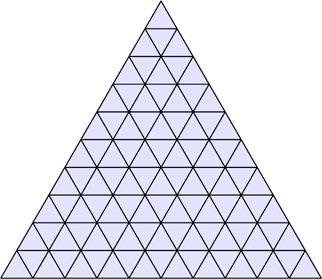 -How many triangles on this pic?
-And how to calculate amount of triangles for arbitrary size of the biggest triangle? (i.e. to find equation for progression a1=1, a2=5, a3=13, a4=27... ax=?).
Correct answers:
*
-How many triangles on this pic?
-And how to calculate amount of triangles for arbitrary size of the biggest triangle? (i.e. to find equation for progression a1=1, a2=5, a3=13, a4=27... ax=?).
Correct answers:
* 

 Well done guys, now one more easy challenge:
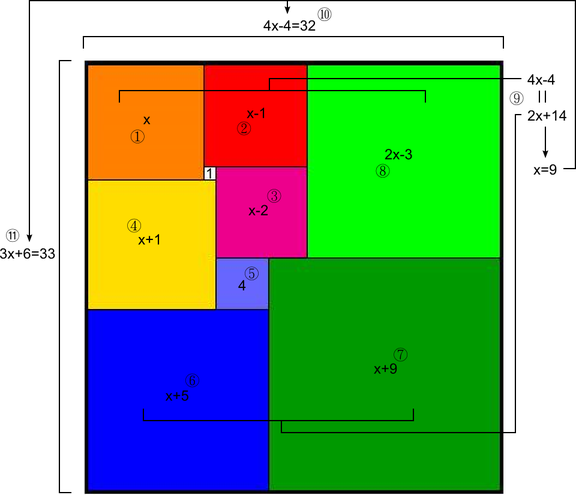
Rectangle was cut into 9 squares as shown in the picture. Size of the smallest white square is 1.
-Find sides of this rectangle.
Well done guys, now one more easy challenge:
Rectangle was cut into 9 squares as shown in the picture. Size of the smallest white square is 1.
-Find sides of this rectangle.
 Ok, problems with triangles and with squares were easily solved. Now time for pentagon!
-Radiuses of all small circles = 1. Find radius of big circle.
---
Ok, problems with triangles and with squares were easily solved. Now time for pentagon!
-Radiuses of all small circles = 1. Find radius of big circle.
---




 By previous question, at the origin we have a smaller circle of radius r, touching the surrounding five of radius R=1. This gives the interior circle a radius of
r = R*(1/(sin(pi/n))-1=1/sin(pi/5)-1= ~0.7 (Yellow)
Distance from origin to inner circle origin D(O,Oi)=r+R=r+1 (Red)
Distance from inner to outer circle origin D(Oi,Oo)=2R=2 (Green)
Distance from outer origin to outer edge D(Oo,E)=R=1 (Green)
But these are obviously not in the same direction, so to find the overall distance we need a bit of trig. First consider the closest triangle, formed by 2 reds and a green. This is isosceles, and we know the inner angle, thus:
A(Oi,O,Oi)=2pi/5
A(Oi,Oi,O)=(pi-2pi/5)/2=(5pi/5-2pi/5)/2=3pi/10
We know the four inner/outer circles create a square, giving
A(Oi,Oi,Oo)=pi/2
A(O,Oi,Oo)=A(Oi,Oi,O)+A(Oi,Oi,Oo)=pi/2+3pi/10=5pi/10+3pi/10=8pi/10=4pi/5
Now we know this angle, we can use it for the larger triangle OoOiO (Green Red Blue). From a2=b2+c2-2bcCos(A), we have
D(O, Oo)2=22+(1+r)^2-2(2)(1+r)Cos(4Pi/5)= ~12.4
D(O, Oo)=L= ~3.52 (Blue)
Next, we have consider triangle OoOOo (blue blue green), being isosceles with lengths L, L, and 2R=2. We need the interior angle, so therefore we have
A(Oo,O,Oo)=ArcCos ((b2+c2-a2)/(2bc))=ArcCos ((L2+L2-22)/(2(L)(L)))=ArcCos ((2L2-4)/(2L2)=ArcCos (1-2/L2)
=~ArcCos(0.84) =~ 0.58 radians.
This gives the other triangles' angles as:
A(O,OO,OO)=(Pi-0.58)/2=~1.28 radians.
A(O,OO,E)=1.28+Pi/2=~2.86 radians.
Finally, consider the triangle going from OOoE (Blue Green Purple). We know 2 lengths, and one angle (2.86), giving our overall radius D (Purple) to be
a2=b2+c2-2bcCos(A)
D2=3.522+12-2(3.52)(1)Cos(2.86)=~20.1
D=~4.49
By previous question, at the origin we have a smaller circle of radius r, touching the surrounding five of radius R=1. This gives the interior circle a radius of
r = R*(1/(sin(pi/n))-1=1/sin(pi/5)-1= ~0.7 (Yellow)
Distance from origin to inner circle origin D(O,Oi)=r+R=r+1 (Red)
Distance from inner to outer circle origin D(Oi,Oo)=2R=2 (Green)
Distance from outer origin to outer edge D(Oo,E)=R=1 (Green)
But these are obviously not in the same direction, so to find the overall distance we need a bit of trig. First consider the closest triangle, formed by 2 reds and a green. This is isosceles, and we know the inner angle, thus:
A(Oi,O,Oi)=2pi/5
A(Oi,Oi,O)=(pi-2pi/5)/2=(5pi/5-2pi/5)/2=3pi/10
We know the four inner/outer circles create a square, giving
A(Oi,Oi,Oo)=pi/2
A(O,Oi,Oo)=A(Oi,Oi,O)+A(Oi,Oi,Oo)=pi/2+3pi/10=5pi/10+3pi/10=8pi/10=4pi/5
Now we know this angle, we can use it for the larger triangle OoOiO (Green Red Blue). From a2=b2+c2-2bcCos(A), we have
D(O, Oo)2=22+(1+r)^2-2(2)(1+r)Cos(4Pi/5)= ~12.4
D(O, Oo)=L= ~3.52 (Blue)
Next, we have consider triangle OoOOo (blue blue green), being isosceles with lengths L, L, and 2R=2. We need the interior angle, so therefore we have
A(Oo,O,Oo)=ArcCos ((b2+c2-a2)/(2bc))=ArcCos ((L2+L2-22)/(2(L)(L)))=ArcCos ((2L2-4)/(2L2)=ArcCos (1-2/L2)
=~ArcCos(0.84) =~ 0.58 radians.
This gives the other triangles' angles as:
A(O,OO,OO)=(Pi-0.58)/2=~1.28 radians.
A(O,OO,E)=1.28+Pi/2=~2.86 radians.
Finally, consider the triangle going from OOoE (Blue Green Purple). We know 2 lengths, and one angle (2.86), giving our overall radius D (Purple) to be
a2=b2+c2-2bcCos(A)
D2=3.522+12-2(3.52)(1)Cos(2.86)=~20.1
D=~4.49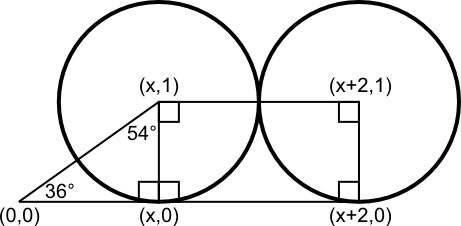 Then x=tan 54° and so the distance from the origin to the center of the outer circle is sqrt(x2+4x+5)=sqrt((tan 54°)2+4(tan 54°)+5)
Therefore, the radius of the big circle (enclosing the outer circles) is one unit more; that is, sqrt((tan 54°)2+4(tan 54°)+5)+1. You can substitute tan 54°=φ/sqrt(3-φ) if you like (φ is the golden ratio (1+sqrt(5))/2), but I won't do that here. The number comes out to be about 4.521, close to Flip's estimate.
Then x=tan 54° and so the distance from the origin to the center of the outer circle is sqrt(x2+4x+5)=sqrt((tan 54°)2+4(tan 54°)+5)
Therefore, the radius of the big circle (enclosing the outer circles) is one unit more; that is, sqrt((tan 54°)2+4(tan 54°)+5)+1. You can substitute tan 54°=φ/sqrt(3-φ) if you like (φ is the golden ratio (1+sqrt(5))/2), but I won't do that here. The number comes out to be about 4.521, close to Flip's estimate.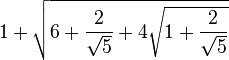 =
= 














