Congratulations, you win the battle for the best program. I did some optimizations to my program (which is essentially brute-forcing the complete puzzle), and it gave me the same solution, but it required several hours for finding it:
counter: 1088987; elements: 18104; max: 46989; unsolvables removed: 396759
* * 5 6 7 8 9 * * *
* - 4 3 2 - 10 11 12 *
* - - - 1 - - - 13 *
* - 48 47 46 - 18 17 14 *
* - - - 45 - 19 16 15 *
* 41 42 43 44 21 20 - - *
* 40 39 38 - 22 25 26 - *
* - - 37 - 23 24 27 - *
* - - 36 35 34 - 28 29 *
* * * * * 33 32 31 30 *
!! best solution found !!
I think your solver works correctly -- and much faster than my one.
EDIT: The program doesn't work correctly for Stage 1:
44 solutions found.
Total solutions found: 52
Fastest solution (22 frames):
* * *-*-* * *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + . $ . *
|
* . + . $ . *
| |
* * *-*-* * *
Shortest solution (16 tiles):
* * *-*-* * *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + . $ . *
|
* . + . $ . *
| |
* * *-*-* * *
script finished running
script stopped.
It fails on stage 3:Best attempt before brute-forcing:
*?*?A?*?A?*?*
? ? ? ?
* . A . A . *
? ? ? ?
* . A . A . *
? ? ? ?
* . A?A?A . *
? ? ?
* . . A . . *
? ? ?
* . . A . . *
? ? ?
* . . A . . *
? ? ?
* . . A . . *
? ? ?
*?*?*?A?*?*?*
0 solutions found.
Total solutions found: 5962
Fastest solution (47 frames):
* * *-*-* * *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + $-+ . *
|
*-+ + . +-+ *
| | | | |
* + + . + + *
| | | | |
* + + . + + *
| | | | |
* +-+ . + $ *
| |
+-*-*-*-* * +
Shortest solution (29 tiles):
* * *-*-* * *
| |
* . + . + . *
| |
* . + . + . *
| |
* . + $-+ . *
|
* +-+ . +-+ *
| | |
* +-+ . + + *
| | |
* +-+ . + + *
| | |
* +-+ . + $ *
| |
+ * *-*-* * +
script finished running
script stopped.
For reference: If the programs are improved even more, it must be at least as good as that for the benchmark:
* * * * * * * 14 13 12
* 21 20 19 18 17 16 15 - 11
23 22 - - - - - - - 10
24 - - - - - - - 8 9
25 - 1 2 3 4 5 6 7 -
26 - - - - - - - 44 43
27 - 51 50 49 48 47 46 45 42
28 - - - - - - - 40 41
29 - 33 34 35 36 37 38 39 *
30 31 32 * * * * * * *
-----------------------------------
Edit: Another good idea would be:
Before you start to brute-force, calculate an estimation on how many frames and how many fields are required at least. For example for the benchmark puzzle it's (3 frames + 4 frames)*(math.min(rows, colums)-1) = 49 frames and sum over all rows i (min(black in row i, white in row i)) = 1*8 = 8.
To measure partial solutions, just add 7 frames * (min(incompletely solved rows, incompletely solved columns) - 1) for minimum score, or #unused fields for minimum fields.
Then when searching for solutions, look on how hard it will be to brute-force. If it might take very long, calculate an estimate and enqueue. First calculate the "easy" solutions which don't require too much brute-force.
Now after you found some "easy" solutions, you can come back to the solutions requiring a lot of brute-force. You should be able to find the solution given above pretty fast. Now that was done: If you can only find solutions which take more fields and more frames than the currently best solution, then throw it away and don't brute-force at all.
example:
Best attempt before brute-forcing:
*-*-*-*-*-*-*-*-* +
| |
* . . . . . . . +-*
| |
*-+ . . . . . . . *
| |
*-+ A?A?A?A?A?A . *
| ? ? ? ? ? ? |
* . A?A?A?A?A?A-+-*
| ? ? ? ? ? ?
*-+-A?A?A?A?A?A . *
? ? ? ? ? ?
* . A?A?A?A?A?A-+-*
? ? ? ? ? ? |
*-+ A?A?A?A?A?A . *
| ? ? ? ? ? ? |
* . A?A?A?A?A?A-+-*
| | | |
*-*-* * *-*-* * * +
This requires 29 turns at least, and ~70 fields. The solution found above requires 18 turns, and 51 fields. It is definitely impossible for this situation to get a better solution than the one above.
-------------------------------------------
Found connections at region edges:
+++++++.
+.......
.......+
+.......
.......+
.aaaaa?+
+!aaaaa.
.??????+
Best attempt before brute-forcing:
A?A?A?A?A?A?A?*?*?*
? ? ? ? ? ? ? | ?
A?A?A?A?A?A?A-+ . *
? | ?
*-+ . . . . . . . *
? ?
* . . . . . . . +-*
? ?
*-+ . . . . . . . *
? ?
* . . . . . . . +-*
? | ?
* . +-B?B?B?B?B?B?B
? | ? ? ? ? ? ?
*-+-+ B?B?B?B?B . *
? ? ? ? ? ? ?
* . +-B?B?B?B?B?B?B
? | ? ? ? ? ? ?
*?*?*?B?B?B?B?B?B B
This should be detected as unsolvable. The reason is easy: Take one starting point. Now solve the top part. If you now continue, then you come across the other endpoint and didn't solve the lower part.
Now take a starting point, and assume you could solve the lower part. You can't get to the top part afterwards without coming across the other endpoint.
------------------------------------
Trying row combination:
1111112.
2.......
.......4
4.......
.......2
.2111111
2111111.
.1111111
0 endpoints available.
If there are already two endpoints, it is safe to assume that every cell which has two forced neighbors is also a forced cell connected to both of them - otherwise it would create an additional endpoint, which is forbidden.
In this case, the 1 at the lowest left would also become a forced cell this way.
---------------------------------
Also: If two rows are completely disconnected, then finding the solution can be split in two parts. For example, in my solution for the benchmark puzzle, the top two rows are disconnected from the rest of the puzzle, so finding the solutions can be split as following:
- solve the top part, use row 2, column 0 as an endpoint, use row 2, column 9 as an endpoint. at the same time: solve the bottom puzzle, use (3,0) and (3,9) as endpoints, allow two additional endpoints anywhere in the bottom part.
- solve the top part using two endpoints, one of them being (2,0). at the same time, solve the bottom part using two endpoints, one of them must be (3,0).
- solve the top part using two endpoints, one of them being (2,9). at the same time, solve the bottom part using two endpoints, one of them must be (3,9).
- solve the top part by using a total of 4 endpoints, two of them are (2,0) and (2,9). solve the bottom part using (3,0) and (3,9) as endpoints.
-----------------------------------------
another edit:
MEM_COLS = 0x020E3F64
MEM_ROWS = 0x020E3FA8
MEM_CELL_ROW1_COL1 = 0x020E03C4
MEM_rowoffset = 0x0140
MEM_coloffset = 0x14
MEM_valoffset = 0x1
function readpuzzle()
local puzzle = {}
local rows = memory.readbyte(MEM_ROWS)
local cols = memory.readbyte(MEM_COLS)
for r = 1, rows do
puzzle[r] = {}
for c = 1, cols do
puzzle[r][c] =
memory.readbyte(
MEM_CELL_ROW1_COL1
+ MEM_rowoffset * (r - 1)
+ MEM_coloffset * (c - 1)
) - MEM_valoffset
end
end
return puzzle
end


 (more) Optimal route I used (131 frames):
(more) Optimal route I used (131 frames):
 I have contacted the creator of the solver to see if they can provide me the source code/help me with making my own solver so will hopefully get a reply, but if not I'll probably need help making my own solver since I'm not the best programmer and I'm not really sure where to start.
I have contacted the creator of the solver to see if they can provide me the source code/help me with making my own solver so will hopefully get a reply, but if not I'll probably need help making my own solver since I'm not the best programmer and I'm not really sure where to start.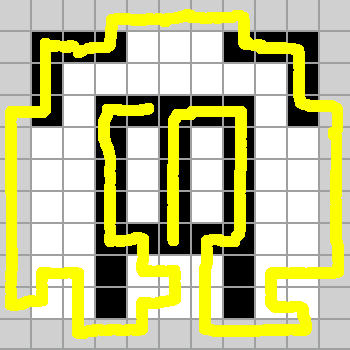
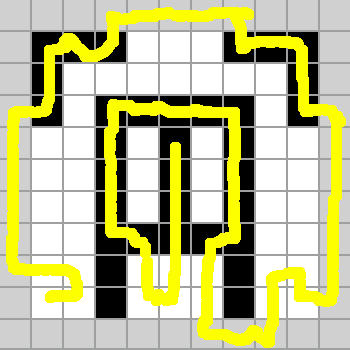
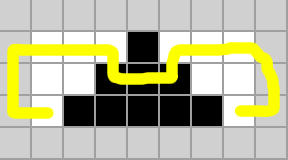
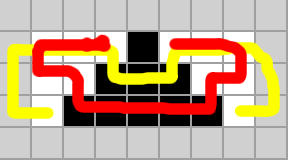 stage 10:
stage 10:
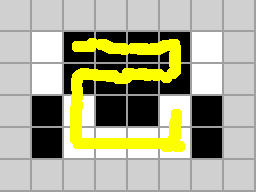 stage 14:
stage 14:
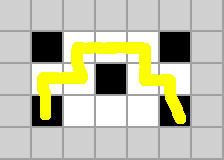 stage 18:
stage 18: 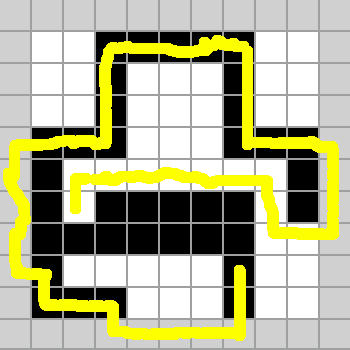 The main idea is to avoid using the outer fields as much as possible. If you can avoid using the outer fields by walking through more fields in the middle this is always a good idea.
The next idea: Try to avoid placing the two ends of the paths too close to each other.
The main idea is to avoid using the outer fields as much as possible. If you can avoid using the outer fields by walking through more fields in the middle this is always a good idea.
The next idea: Try to avoid placing the two ends of the paths too close to each other.