Well, it's been here long enough. The method to solve:
Because of the small concavity, any force that will act during the collision will be applied at the new axis of rotation. Thus, there won't be any torque with relation to this axis and angular momentum will be conserved. From this relation, we can get the ratio of the angular velocity of the prism before the impact to the one after it. Since there's no sliding, the prism only rotates and its kinetic energy is only rotational and proportional to the square of its angular velocity. From this, we get the ratio of energy lost during the collision.
We're also able to deduce the relation of the kinetic energy of the pencil immediately before the (n+1)th collision to the energy immediately before the nth collision. It can be seen as the amount of energy that didn't dissipate in the collision plus the potential energy it gained while going down the plane.
We find the limit of the kinetic energy as n goes to infinity. If this limit is too small, the prism will eventually hit the plane, lose some energy and won't have enough mechanical energy to lift its center of mass to the highest point and won't be able to continue its movement. Therefore, the smallest angle is the one that gives just enough asymptotic kinetic energy to lift the pencil after a collision. This final equation will give the angle.
The execution is not as pretty. First of all, the angular momentum of a rigid body is intimately related to its moment of inertia, so we have to calculate it for the pencil. To do this, instead of considering an hexagon with a central axis, we calculate the moment of inertia for a regular triangular prism rotating along its edge and multiply the result by six. So, considering the edge of the hexagonal of length a, its density rho and its longitudinal length L, the moment of inertia is given by the double integral:
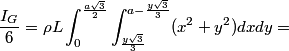
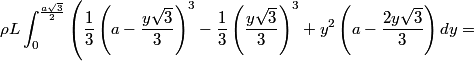
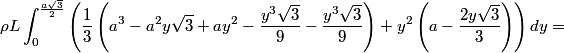


It's convenient to express it in function of the mass, so by using the formula for the volume of an hexagonal prism:
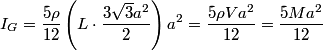
Using Steiner's theorem, we find the moment for the rotation about one of the pencil's edges:
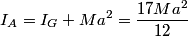
Now we're ready to analyze the motion. The following pictures show the pencil before, during and after a collision, respectively:
http://i992.photobucket.com/albums/af49/p4wn3r/hexagonbefore.png
http://i992.photobucket.com/albums/af49/p4wn3r/hexagonduring.png
http://i992.photobucket.com/albums/af49/p4wn3r/hexagonafter.png
Notice that point B is at rest before the collision, so it suffers no force from the plane. The small concavity implies that all interaction will occur at point A only, and since collisions take short time, force Fc is much larger than the weight, normal and static friction. In a theoretical situation where they take infinitesimal time, the effect of those other forces is zero and we can assume that only Fc is acting during the collisions. Thus, we can find a relation between the two rotating movements noticing that angular momentum is conserved with respect to A.
So, we calculate the angular momentum before the collision. It can be seen as the addition of the angular momentum about the center of mass plus the momentum the prism would cause in A if its mass were all shrunk in its center of mass:
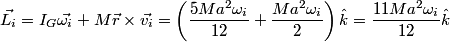
The angular momentum after is easier to find, because it's only a rotation about A:
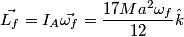
From the equality of these formulas, we get that the ratio of angular velocities after the collision is 11/17. Since K = I omega^2 / 2, we get the amount of energy that dissipated:

Let K_n denote the energy immediately before the nth collision. Before the (n+1)th collision, it'll have 121/289 of the energy it had before plus the potential energy it gained from the descent of the center of mass. Geometrically, after a 60º revolution, the center of the hexagon is a distance of "a" units from where it was before, on a line inclined \theta from the horizontal. So, the vertical descent of it is a*sin(theta) and:
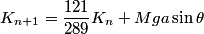
It can be proved that, for small enough angles, this sequence converges (you can solve the linear recurrence or prove it's bounded and monotonic after a certain point). Say that the limit is K, then:

Finally, we notice that, for the movement to continue, K cannot be too small. At the smallest angle, the kinetic energy the prism has after hitting the plane is just enough to give it enough potential energy to lift its center of mass to the highest position in the trajectory. Geometrically, we can see that the segment OA is (30º-\theta) from the vertical. When it rotates, the difference of height of the center will be a(1-cos(\theta)). By equaling the remaining kinetic energy after collision with the potential energy to lift it this high, we get the final equation (I use u=121/168):
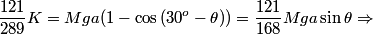
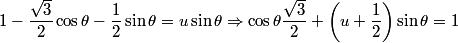
This last equation can be solved as any other type of a cos(x) + b sin (x) = c . We divide it by sqrt(a^2+b^2) and now the coefficients multiplying sin and cos obey the fundamental trigonometric relation and are the sine and cosine of another angle, and we can simplify it applying the sin(a+b) formula.
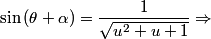
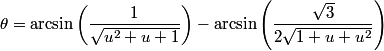
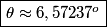
I know many other physics problems whose solutions will make this one look very small :P









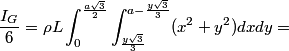
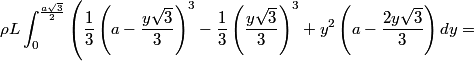
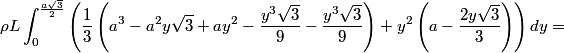

 It's convenient to express it in function of the mass, so by using the formula for the volume of an hexagonal prism:
It's convenient to express it in function of the mass, so by using the formula for the volume of an hexagonal prism:
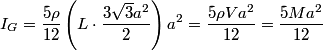 Using Steiner's theorem, we find the moment for the rotation about one of the pencil's edges:
Using Steiner's theorem, we find the moment for the rotation about one of the pencil's edges:
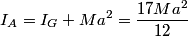 Now we're ready to analyze the motion. The following pictures show the pencil before, during and after a collision, respectively:
Now we're ready to analyze the motion. The following pictures show the pencil before, during and after a collision, respectively:
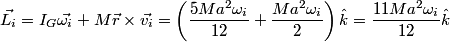 The angular momentum after is easier to find, because it's only a rotation about A:
The angular momentum after is easier to find, because it's only a rotation about A:
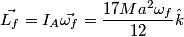 From the equality of these formulas, we get that the ratio of angular velocities after the collision is 11/17. Since K = I omega^2 / 2, we get the amount of energy that dissipated:
From the equality of these formulas, we get that the ratio of angular velocities after the collision is 11/17. Since K = I omega^2 / 2, we get the amount of energy that dissipated:
 Let K_n denote the energy immediately before the nth collision. Before the (n+1)th collision, it'll have 121/289 of the energy it had before plus the potential energy it gained from the descent of the center of mass. Geometrically, after a 60º revolution, the center of the hexagon is a distance of "a" units from where it was before, on a line inclined \theta from the horizontal. So, the vertical descent of it is a*sin(theta) and:
Let K_n denote the energy immediately before the nth collision. Before the (n+1)th collision, it'll have 121/289 of the energy it had before plus the potential energy it gained from the descent of the center of mass. Geometrically, after a 60º revolution, the center of the hexagon is a distance of "a" units from where it was before, on a line inclined \theta from the horizontal. So, the vertical descent of it is a*sin(theta) and:
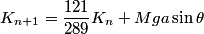 It can be proved that, for small enough angles, this sequence converges (you can solve the linear recurrence or prove it's bounded and monotonic after a certain point). Say that the limit is K, then:
It can be proved that, for small enough angles, this sequence converges (you can solve the linear recurrence or prove it's bounded and monotonic after a certain point). Say that the limit is K, then:
 Finally, we notice that, for the movement to continue, K cannot be too small. At the smallest angle, the kinetic energy the prism has after hitting the plane is just enough to give it enough potential energy to lift its center of mass to the highest position in the trajectory. Geometrically, we can see that the segment OA is (30º-\theta) from the vertical. When it rotates, the difference of height of the center will be a(1-cos(\theta)). By equaling the remaining kinetic energy after collision with the potential energy to lift it this high, we get the final equation (I use u=121/168):
Finally, we notice that, for the movement to continue, K cannot be too small. At the smallest angle, the kinetic energy the prism has after hitting the plane is just enough to give it enough potential energy to lift its center of mass to the highest position in the trajectory. Geometrically, we can see that the segment OA is (30º-\theta) from the vertical. When it rotates, the difference of height of the center will be a(1-cos(\theta)). By equaling the remaining kinetic energy after collision with the potential energy to lift it this high, we get the final equation (I use u=121/168):
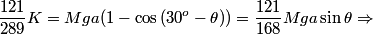
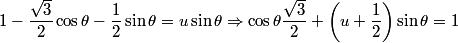 This last equation can be solved as any other type of a cos(x) + b sin (x) = c . We divide it by sqrt(a^2+b^2) and now the coefficients multiplying sin and cos obey the fundamental trigonometric relation and are the sine and cosine of another angle, and we can simplify it applying the sin(a+b) formula.
This last equation can be solved as any other type of a cos(x) + b sin (x) = c . We divide it by sqrt(a^2+b^2) and now the coefficients multiplying sin and cos obey the fundamental trigonometric relation and are the sine and cosine of another angle, and we can simplify it applying the sin(a+b) formula.
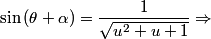
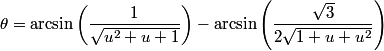
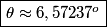 I know many other physics problems whose solutions will make this one look very small :P
I know many other physics problems whose solutions will make this one look very small :P




