I couldn't find a software that could do a triple integral on something that's not a box, so I implemented one myself (probably not as precise as it could be):
http://pastebin.com/k8RTmBsR
This code is able to integrate n-dimensional integrals, experienced programmers should be able to quickly modify it to calculate the gravity field at any point. The present code outputs:
Point A
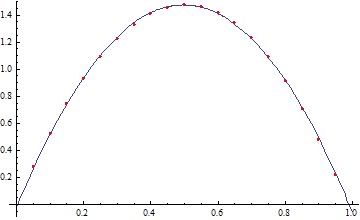
Ratio 0.05 : ( 0.2795 , 0.0000 , -0.0000 )
Ratio 0.10 : ( 0.5272 , -0.0000 , -0.0000 )
Ratio 0.15 : ( 0.7439 , 0.0000 , -0.0000 )
Ratio 0.20 : ( 0.9320 , -0.0000 , 0.0000 )
Ratio 0.25 : ( 1.0927 , -0.0000 , 0.0000 )
Ratio 0.30 : ( 1.2260 , -0.0000 , -0.0000 )
Ratio 0.35 : ( 1.3317 , -0.0000 , -0.0000 )
Ratio 0.40 : ( 1.4095 , 0.0000 , 0.0000 )
Ratio 0.45 : ( 1.4585 , 0.0000 , 0.0000 )
Ratio 0.50 : ( 1.4778 , 0.0000 , -0.0000 )
Ratio 0.55 : ( 1.4661 , 0.0000 , 0.0000 )
Ratio 0.60 : ( 1.4228 , -0.0000 , -0.0000 )
Ratio 0.65 : ( 1.3465 , -0.0000 , -0.0000 )
Ratio 0.70 : ( 1.2377 , -0.0000 , -0.0000 )
Ratio 0.75 : ( 1.0949 , 0.0000 , 0.0000 )
Ratio 0.80 : ( 0.9189 , 0.0000 , 0.0000 )
Ratio 0.85 : ( 0.7124 , 0.0000 , -0.0000 )
Ratio 0.90 : ( 0.4792 , 0.0000 , -0.0000 )
Ratio 0.95 : ( 0.2233 , -0.0000 , 0.0000 )
Point B
Ratio 0.05 : ( -0.0300 , -0.0000 , -0.3079 )
Ratio 0.10 : ( -0.0981 , 0.0000 , -0.6236 )
Ratio 0.15 : ( -0.1916 , 0.0000 , -0.9412 )
Ratio 0.20 : ( -0.3034 , -0.0000 , -1.2608 )
Ratio 0.25 : ( -0.4283 , -0.0000 , -1.5823 )
Ratio 0.30 : ( -0.5622 , 0.0000 , -1.9055 )
Ratio 0.35 : ( -0.7019 , 0.0000 , -2.2300 )
Ratio 0.40 : ( -0.8442 , 0.0000 , -2.5553 )
Ratio 0.45 : ( -0.9870 , -0.0000 , -2.8808 )
Ratio 0.50 : ( -1.1280 , -0.0000 , -3.2058 )
Ratio 0.55 : ( -1.2656 , -0.0000 , -3.5296 )
Ratio 0.60 : ( -1.3981 , -0.0000 , -3.8511 )
Ratio 0.65 : ( -1.5244 , -0.0000 , -4.1698 )
Ratio 0.70 : ( -1.6433 , 0.0000 , -4.4846 )
Ratio 0.75 : ( -1.7543 , 0.0000 , -4.7950 )
Ratio 0.80 : ( -1.8568 , -0.0000 , -5.1000 )
Ratio 0.85 : ( -1.9502 , 0.0000 , -5.3991 )
Ratio 0.90 : ( -2.0346 , -0.0000 , -5.6915 )
Ratio 0.95 : ( -2.1094 , -0.0000 , -5.9767 )
C++ has an awful habit of printing -0.0000 . I told it to evaluate the zero values to check its correctness. The components of the vectors, when multiplied to G*\mu*R, where G is the gravitational constant, \mu the torus density and R the largest radius, will yield the acceleration caused by gravity at that point. We can see that the torus world is very unstable at B, with some nasty pulls towards the center. I plotted A's x components and could get a great fit with a parabola:


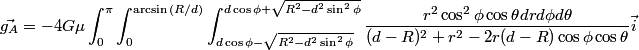
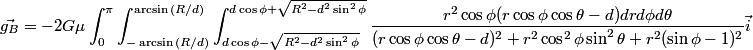
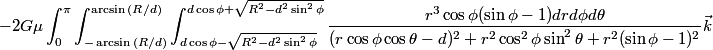 I cannot guarantee that the integrals have finite form primitives, perhaps someone could fill some values and evaluate them numerically to see the direction the vectors point?
EDIT: Does anyone want to know the math behind this? I think it's very annoying...
EDIT 2: I keep confusing R with r!!!!
In the last two integrals, r^2 (sin fi - 1) read r^2 sin fi - R^2. And in the third, r^3 (sin fi - 1) = r^2 ( r sin fi - R)
I cannot guarantee that the integrals have finite form primitives, perhaps someone could fill some values and evaluate them numerically to see the direction the vectors point?
EDIT: Does anyone want to know the math behind this? I think it's very annoying...
EDIT 2: I keep confusing R with r!!!!
In the last two integrals, r^2 (sin fi - 1) read r^2 sin fi - R^2. And in the third, r^3 (sin fi - 1) = r^2 ( r sin fi - R)


