Welcome, this is the discussion board of TASVideos.
If you have a question, please read the Site FAQ first to see if your question has already been answered.
Be sure your posts conform to Site Rules
We also have a Discord server and an IRC channel #tasvideos at irc.libera.chat...
Be sure your posts conform to Site Rules
We also have a Discord server and an IRC channel #tasvideos at irc.libera.chat...
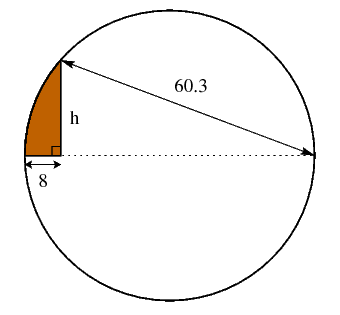 1) Calculate the area of the shaded part.
2) Take the integral part of the result, negate it, and use it as longitude coordinates, in degrees. Take the two first digits after the decimal point of the area and use them as latitude coordinates in degrees. (Mathematically speaking, if the area is A, then latitude = floor((A - floor(A))*100) degrees.)
3) These coordinates will point to a state in the US. Y = the year when the capital city of this state was founded.
4) Take Y modulo 100 (iow. the last two digits) and substitute the 60.3 in the picture with this value.
5) The answer to the problem is the height h using this modified value, with at least 5 decimals of accuracy (after the decimal point).
1) Calculate the area of the shaded part.
2) Take the integral part of the result, negate it, and use it as longitude coordinates, in degrees. Take the two first digits after the decimal point of the area and use them as latitude coordinates in degrees. (Mathematically speaking, if the area is A, then latitude = floor((A - floor(A))*100) degrees.)
3) These coordinates will point to a state in the US. Y = the year when the capital city of this state was founded.
4) Take Y modulo 100 (iow. the last two digits) and substitute the 60.3 in the picture with this value.
5) The answer to the problem is the height h using this modified value, with at least 5 decimals of accuracy (after the decimal point).


 [/URL]
if you plot it with bins of width 1 its a bit useless to look at...
edit: ps I assumed roll(0,0) = 0
[/URL]
if you plot it with bins of width 1 its a bit useless to look at...
edit: ps I assumed roll(0,0) = 0
