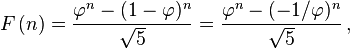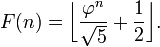An array is a continuous section of memory containing data of the same type. An array of 10 ints, which are often 4 bytes long, would be a section of memory 40 bytes long. C only cares about where in memory that section starts, so if you have a pointer to the first element of the array, that is all you need to know. This means that arrays and pointers are interchangeable, basically.
To create an array, you may write
int a[10] = {0,1,2,3,4,5,6,7,8,9};
When you do this, a section of memory (on the stack) will be filled with these numbers. In a hex editor, it might look like:
0 1 2 3 4 5 6 7 8 9 A B C D E F
00 25 50 44 46 2D 31 2E 32 0A 25 E2 E3 CF D3 0D 0A
10 32 20 30 20 00 00 00 00 01 00 00 00 02 00 00 00
20 03 00 00 00 04 00 00 00 05 00 00 00 06 00 00 00
30 07 00 00 00 08 00 00 00 09 00 00 00 6F 64 65 20
40 2F 46 6C 61 74 65 44 65 63 6F 64 65 5D 0A 3E 3E
Here, the array starts at position 0x14 in memory, so the variable a will have this value in this case. To look up a value in the array, you do
int b = a[3];
for example. This means: Go to the address contained in a. Add 3 times the size of an integer to that address, and read an integer from it, storing it in b. Doing this, we find: a = 0x14. sizeof(int) = 4, so a+3*sizeof(int) = 0x14 + 0xC = 0x20, where we find the integer value 3, as expected. This makes it easy to see what would happen if we ask for something at a greater position than what was allocated for the array. We just get whatever lies in memory afterward. In this example, a[10] would read the bytes 5D 0A 3E 3E which corresponds to the integer 1044253277. C does not keep track of how long the array actually is.
Any pointer can be treated as an array. For example
int * c = a+6;
return c[3];
This will return the same thing as a[9]. c is a pointer to a place in memory 6*sizeof(int) later in memory than a, that is 0x2C, and we can treat this as an array starting at a later point in the original array a.
Another way of creating an array is to use malloc to reserve an area of memory on the heap:
int * d = malloc(1000*sizeof(int));
This can be used just like the previous arrays, except that you should free up the memory after you're done with it:
free(d);
(this will happen automatically when your program exits, though, so for a small program it is not a disaster if you forget).
And as for what they are useful for, isn't that pretty obvious? Let's say that you want to read in 10 numbers from standard input, and print them back their squares in reverse order. Without arrays, this would look like
int a,b,c,d,e,f,g,h,i,j;
scanf("%d%d%d%d%d%d%d%d%d%d",
&a, &b, &c, &d, &e, &f, &g, &h, &i, &j);
printf("%d\n%d\n%d\n%d\n%d\n%d\n%d\n%d\n%d\n%d\n",
j*j,i*i,h*h,g*g,f*f,e*e,d*d,c*c,b*b,a*a);
and would look even uglier with more numbers or more complicated operations. With arrays, it would look like:
int i, a[10];
for(i = 0; i < 10; i++) scanf("%d", a+i);
for(i = 9; i >= 0; i--) printf("%d\n", a[i]*a[i]);
Much cleaner, right?