Ok, in this post I will try to explain how the new ranking system works. It will be a little similar to my previous post explaining this, but I'll add the specifics:
The following formula will give a result for all players with a published movie:
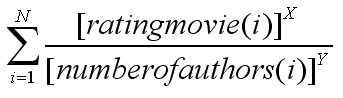
- Take the rating of one of your published movies to the power of X.
- Divide it by the number of authors of that movie to the power of Y.
- Do this for all your published movies and add the numbers you get, this will give you your result.
- N is your total amount of published movies.
- X should be determined on how important high ratings are considered. For instance, if X=0, then ratings don't matter at all, and only the amount of movies is considered. If X=1, you will just be adding the ratings of your movies. If X is bigger than 1, movies with higher ratings will count heavier. It is probably good if X is bigger 1, since generally, one movie with a rating of 9.0 is liked better than two movies with a rating of 4.5
- Y should be determined by how much team movies count. If Y=0, the authors will both get the full amount of points for the movie, the same amount an author would get if he had made the movie alone. If Y=1, you divide the amount of points a movie would get equally of the authors. The most logical value for Y is probably somewhere between 0 and 1.
- Lets call the result of the summation Z.
Now that every player with a published movie has a result, these results can be listed. This is done
here You will need to put in values for X and Y in order to change the list.
Once X and Y are determined, certain ranges of results must be grouped together if the result is:
Bigger than 0, smaller than A --> rank 1
Bigger than A, smaller than B --> rank 2
.....
Bigger than E --> rank 5
Then the names of those ranks needed to be determined.
===============================================
Specifics:
Determining X:
As already stated, X needs to be higher than 1 to account for the fact that a single movie rated a 9 is appreciated more than two movies rated a 4.5. One can ask him/herself the question: How many movies rated a 5 are worth a movie I would rate a 10? Or, 100 movies rated a 9 are worth howmany movies rated an 8? Here are some answers to those questions for several X values:
X=2: 4 of your 5 ratings are worth one 10 rating, 100 of your 9 ratings are worth 126 of your 8 ratings
X=2.5: 5.5 of your 5 ratings are worth one 10 rating, 100 of your 9 ratings are worth 134 of your 8 ratings
X=3: 8 of your 5 ratings are worth one 10 rating, 100 of your 9 ratings are worth 142 of your 8 ratings
X=3.5: 11.3 of your 5 ratings are worth one 10 rating, 100 of your 9 ratings are worth 151 of your 8 ratings
X=4: 16 of your 5 ratings are worth one 10 rating, 100 of your 9 ratings are worth 160 of your 8 ratings
After some thought, and asking some opinions, I determined that X = 2.5 seems like an appropriate value.
Determining Y
As stated before: "If Y=0, the authors will both get the full amount of points for the movie, the same amount an author would get if he had made the movie alone. If Y=1, you divide the amount of points a movie would get equally of the authors. The most logical value for Y is probably somewhere between 0 and 1."
At Y = 0.5, it means that for being a part of a 4-player movie, you half the score you would get from it if you have made that movie alone.
If you made a 2-player team movie, you will get about 0.7 times the score of what you would have gotten if you made this TAS on your own.
These two values of X=2.5 and Y=0.5 seems reasonable, and create
the following list.
Here is a table that tells you which ratings will add howmany points to your score with X=2.5, and what fraction of those points you will get in a teammovie with Y=0.5:
Rating: Score: Players: Fraction:
0.0 0.00 1 1.0000
0.5 0.18 2 0.7071
1.0 1.00 3 0.5774
1.5 2.76 4 0.5000
2.0 5.66 5 0.4472
2.5 9.88
3.0 15.59
3.5 22.92
4.0 32.00
4.5 42.96
5.0 55.90
5.5 70.94
6.0 88.18
6.5 107.72
7.0 129.64
7.5 154.05
8.0 181.02
8.5 210.64
9.0 243.00
9.5 278.17
10.0 316.23
Determining the ranges:
Obsoleted movies will have their score multiplied by a really low number. This way, they are still accounted for, and people without any currently published movies can still get a player rank. These would have a result between 0 and 1.
People with a single published movie will get the player rank. The question would be, from what result they would go one rank up. Eventually it was determined that a result of 250 would be a good value. To get 250, you either need 3 movies with 5.8, 2 movies with 6.9 or 1 movie with 9.1. This seemed like a good requirement to move on a rank. So the player rank was is given at values from 1 - 250
The next rank you get when you double that, at 500, and the next again when you double it to 1000, and finally when you double to to 2000. The list of the result for all player gave a somewhat exponential curve, so even though the ranges get higher, the amount of people occupying the ranks get lower.
After that the names of the ranks had to be thought up. Here are the results of this, listed with the amount of people at this moment:
0 < Z < 1: 51 people - Former Player
1 < Z < 250: 111 people - Player
250 < Z < 500: 33 people - Active Player
500 < Z < 1000: 22 people - Experienced Player
1000 < Z < 2000: 7 people - Skilled Player
2000 < Z : 5 people - Expert Player
You can also somewhat see the people with their ranks
here.
(Note that the table for instance says 5 expert players, and the page only say 4, which is due to Nitsuja currently being labelled a "Coder".)

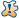





















 - Take the rating of one of your published movies to the power of X.
- Divide it by the number of authors of that movie to the power of Y.
- Do this for all your published movies and add the numbers you get, this will give you your result.
- N is your total amount of published movies.
- X should be determined on how important high ratings are considered. For instance, if X=0, then ratings don't matter at all, and only the amount of movies is considered. If X=1, you will just be adding the ratings of your movies. If X is bigger than 1, movies with higher ratings will count heavier. It is probably good if X is bigger 1, since generally, one movie with a rating of 9.0 is liked better than two movies with a rating of 4.5
- Y should be determined by how much team movies count. If Y=0, the authors will both get the full amount of points for the movie, the same amount an author would get if he had made the movie alone. If Y=1, you divide the amount of points a movie would get equally of the authors. The most logical value for Y is probably somewhere between 0 and 1.
- Lets call the result of the summation Z.
Now that every player with a published movie has a result, these results can be listed. This is done
- Take the rating of one of your published movies to the power of X.
- Divide it by the number of authors of that movie to the power of Y.
- Do this for all your published movies and add the numbers you get, this will give you your result.
- N is your total amount of published movies.
- X should be determined on how important high ratings are considered. For instance, if X=0, then ratings don't matter at all, and only the amount of movies is considered. If X=1, you will just be adding the ratings of your movies. If X is bigger than 1, movies with higher ratings will count heavier. It is probably good if X is bigger 1, since generally, one movie with a rating of 9.0 is liked better than two movies with a rating of 4.5
- Y should be determined by how much team movies count. If Y=0, the authors will both get the full amount of points for the movie, the same amount an author would get if he had made the movie alone. If Y=1, you divide the amount of points a movie would get equally of the authors. The most logical value for Y is probably somewhere between 0 and 1.
- Lets call the result of the summation Z.
Now that every player with a published movie has a result, these results can be listed. This is done