Here's a solution by inversion geometry (circle inversion).
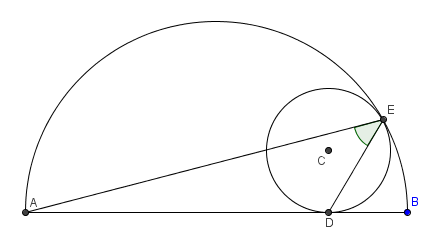
Take p4wn3r's image above, extend semicircle AB to a circle, extend diameter AB to a line, and erase C from all existence, just for fun. Now invert with center E (doesn't matter which radius) and you get something like the following:
Note:
- A maps to A', B to B', D to D'. We don't care what E maps to. E is just E.
- The outer circle through A, B, E maps to the inner line through A'B'. The inner circle through D, E maps to the outer line through D'. Both lines are parallel. This is because, in the original, both circles are tangent at E.
- The line through AB (through D) maps to the circle through E, A', D', B'. E is on the opposite side of A'B' from D', since the original line has A, D, B in that order.
- Furthermore, this circle is special. It is tangent to the outer line at D', since the original line is tangent to the inner circle at D. As well, A'B' is its diameter, since AB is the diameter of the outer circle in the original, and inversion preserves angles (angles formed locally by intersecting curves are preserved).
- Finally, the lines through A'E and through D'E are fixed under inversion, so angle A'ED'= angle AED.
Now, since the lines are parallel, with one going through the diameter A'B' and the other tangent at D', the arc A'D' must be a 90° arc. Make a point G diametrically opposite D'. Then angle A'GD' must be 45°. So angle A'ED' = 45°. From what was said above, angle AED = angle A'ED' = 45°.
I wonder what a solution without inversion geometry looks like. I suppose p4wn3r has one.
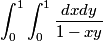Suggestion: Use a change of variables that rotates the axes by an angle of 45º
Bonus points if you can see the mathematical importance of the result of this integral.
